W pewnym uproszczeniu tensor możemy sobie
wyobrażać jako operator działający na wektor i produkujący z niego
nowy wektor o innym zwrocie, kierunku i wartości.
tensor -działający na- wektor = nowy_wektor
Operacja działania tensorem na wektor to coś więcej niż mnożenie
wektora przez liczbę (taka operacja nie zmienia kierunku wektora), więcej
niż mnożenie wektorowe wektorów (bo wtedy otrzymujemy zawsze wektor
prostopadły do płaszyczyzny wyznaczonej przez wektory wyjściowe) i coś
zupełnie innego niż mnożenie skalarne wektorów, czy znajdowanie
wartości wektora (bo z tych ostatnich operacji w wyniku otrzymujemy
skalar).
Matematycznie tensor przedstawia się w postaci macierzy - czyli
specjalnej tablicy składowych. Np. tensor działający na wektorach 3
wymiarowych ma postać tablicy 3 x 3 - ma 9 składowych, z których każda
ma jakiś wpływ na postać wektora wynikowego.
Przykład działania tensora na wektor 2 wymiarowy:
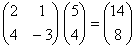
A oto przykład sytuacji, do opisu której niezbędny jest tensor:
wyobraźmy sobie, że chcemy opisywać siłę jaka działa zwrotnie
(reakcja) po zadziałaniu naszą siłą na jakąś powierzchnię. My możemy
działać jakąś siłą w kierunku A, ale ponieważ powierzchnia może
być ustawiona pod kątem, może sprężynować, może być mniej lub
bardziej śliska, więc reakcja tej powierzchni może być pod niemal
dowolnym kątem w stosunku do kierunku siły pierwotnej, może powodować
poślizg, czy skręcenie.
|